Bubble Sort (Elementary Sorting)
Relatively slow sorting algorithm, that does in-place sorting (sorts the array itself) and does not generate additional instances. The avg. time complexity is O(N^2), which is slow!
Description
Start from the beginning (index=0), compare the element with the next, if it’s larger than next => swap positions, if it’s not, then proceed with the next element. At the end of the first iteration, the largest element will be placed at the last position. At the end of the second iteration, the second largest element will be placed (on the last position -1) and so on until we hit the first position, where should be the MIN element.
Runtime Characteristics
2 embedded loops => time complexity is O(N^2)
Pros
- In-place sorting, does not generate new objects (no additional memory usage)
- The fastest on an extremely small and/or nearly sorted set of data
- Better than Selection Sort
Cons
- Not really fast
- Not appropriate for large data sets
- Prefer Insertion Sort over Bubble Sort
Properties
- Stable
- O(1) extra space
- O(n^2) comparisons and swaps
- Adaptive: O(n) when nearly sorted
Usage
- Not used in practise, because of it’s runtime except the cases of very small amount of data, that is almost sorted
Animations, illustrating the algorithm

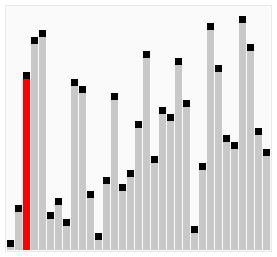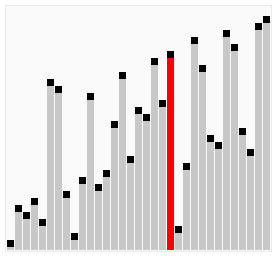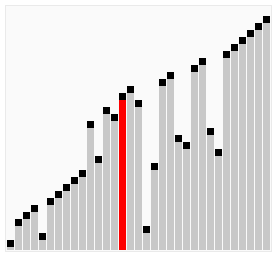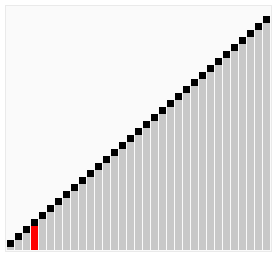
Implementation
public static int[] sort(int[] arr) {
if (arr == null || arr.length == 0 || arr.length == 1) {
return arr;
}
int tmp;
int n = arr.length - 1;
for (int x = 0; x < n; x++) {
for (int y = 0; y < n - x; y++) {
if (arr[y] > arr[y + 1]) {
tmp = arr[y];
arr[y] = arr[y + 1];
arr[y + 1] = tmp;
}
}
}
return arr;
}
Example
Initial: [9, 1, 6, 2, 5, 3, 7]
[1, 9, 6, 2, 5, 3, 7]
[1, 6, 9, 2, 5, 3, 7]
[1, 6, 2, 9, 5, 3, 7]
[1, 6, 2, 5, 9, 3, 7]
[1, 6, 2, 5, 3, 9, 7]
[1, 6, 2, 5, 3, 7, 9]
[1, 2, 6, 5, 3, 7, 9]
[1, 2, 5, 6, 3, 7, 9]
[1, 2, 5, 3, 6, 7, 9]
[1, 2, 3, 5, 6, 7, 9]
Sorted: [1, 2, 3, 5, 6, 7, 9]