The Big O Notation (aka Time/ Memory Complexity)

This is a mechanism to measure the efficiency of a program in context of speed or memory usage. When it comes to speed, it is also called “time complexity” of the algorithm.

Complexity types:

Constant Time - O(1) : Random Access (By Index)

The fastest one. It always takes a constant time to do something, regardless the number of the elements in the collection.

I.e. To access to element in an array by it’s index.

Logarithmic Time - O(log N) : Search Algorithms (In Sorted Collections)

Runtime grows logarithmically in proportion to n.

 for (x = n; x >= 1; x = x/2) {
        console.log(x);
    }

I.e. if it takes 1 second to compute 10 elements, it will take 2 seconds to compute 100 elements, 3 seconds to compute 1000 elements, and so on. An example is the binary search.

Linear Time - O(N) : Looping a collection

We have linear time, when the complexity depends on the number of the elements. If the number of elements increases/ decreases, the time also increases/ decreases with the same rate (linearly).

If you loop a 1/2 of the collection, it’s still a linear time O(N). O(N/2) = O(N)
If you loop a collection 3 times independently, it is still a linear time O(N). O(3N) = O(N)
If you loop two different collections in a single algorithm, you should add their times: O(N + M)

 for (x = 0; x < n; x++) {
        console.log(x);
    }

I.e. when we have to iterate the elements of a collection to do/ find something i.e. to find an element in an array.

Quasilinear Time - O(N log N) or Superlinear algorithm : Sorting algorithms

I.e. when each element have to be compared with every other element.

Quadratic Time - O(N^2) : Nesting loops

When you have nested loops ON THE SAME COLLECTION, then the power depends on the count of the nested loops O(N^2) or O(N^3) and so on…
When you have nested loops ON TWO DIFFERENT COLLECTIONS, then time will be O(N * M).
When you have nested loops ON THREE DIFFERENT COLLECTIONS, then time will be O(N * M * P) and so on.

Power of 2 => O(n^2):

for(){
    for(){
    
    }
}

Power of 3 => O(n^3):

for(){
    for(){
        for(){
        
        }
    }
}

Exponential Time - O(2^n) / 0(N!)

We have exponential time, when the complexity depends on the number of the elements. If the number of elements increases/ decreases, the time also increases/ decreases with double rate.

I.e. when a function calls itself twice (recursion when calculating fibonacci) or iterating binary trees (because they have 2 paths - left & right)

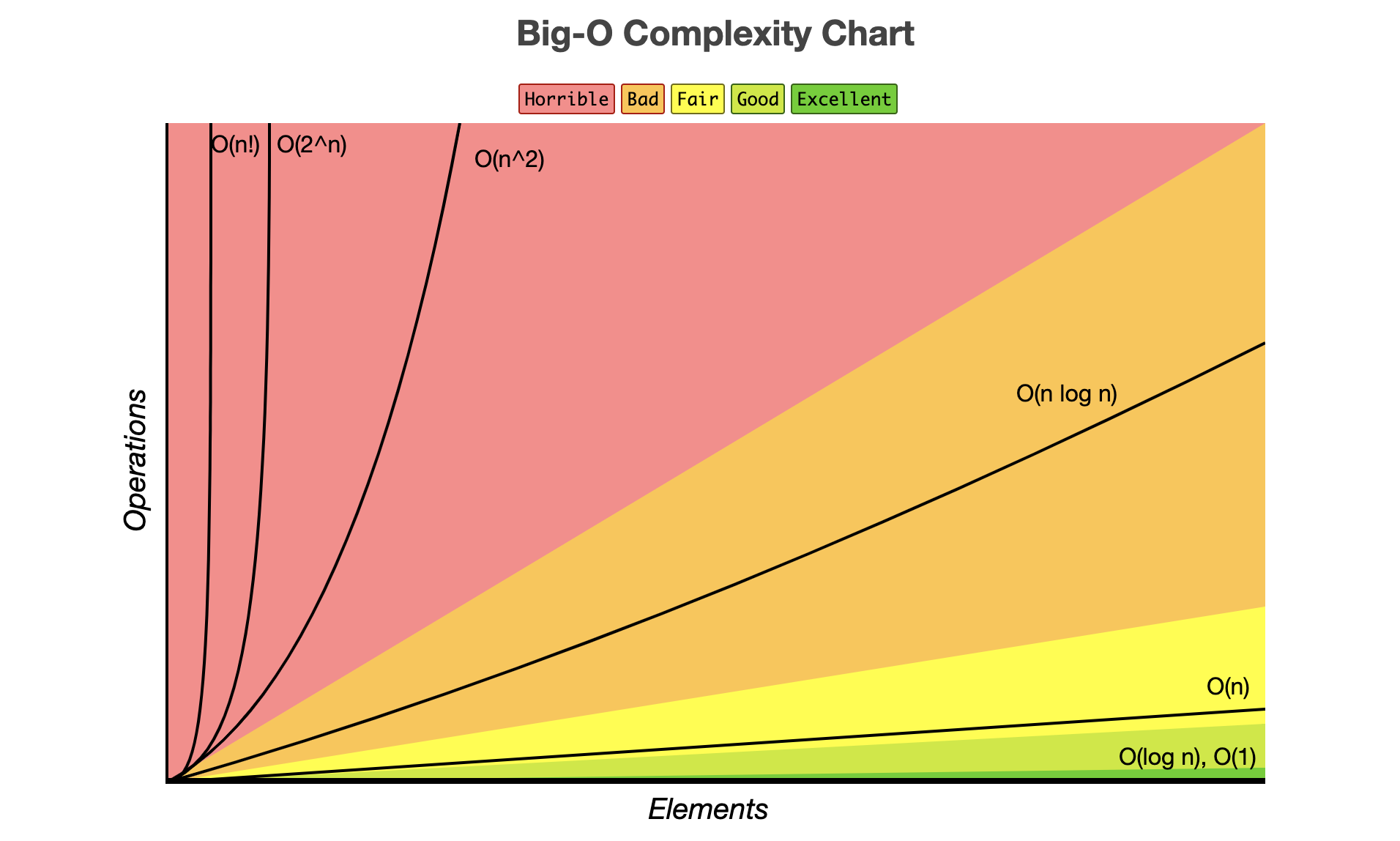
Ordering (from fastest to slowest):

1). Constant: O(1), Logarithmic: O(log n)

2). Linear: O(n)

3). O(n log n)

4). Exponential: O(n^2)

5). Exponential: O(n^3)

6). Exponential: O(2^n)

7). Exponential/ Factorial: O(n!)

Exponential times are really slow! Try to optimize them!

Rules when calculating:

Drop the constants: O(3N) -> O(N)
Drop non-dominant:
- O(N + N^2) -> O(N^2)
- O(M + N) -> O (N) (if we know something about both collections and we know which is dominant, if not - we should leave both)

We consider as a dominant, the one that has more elements or needs the most operations

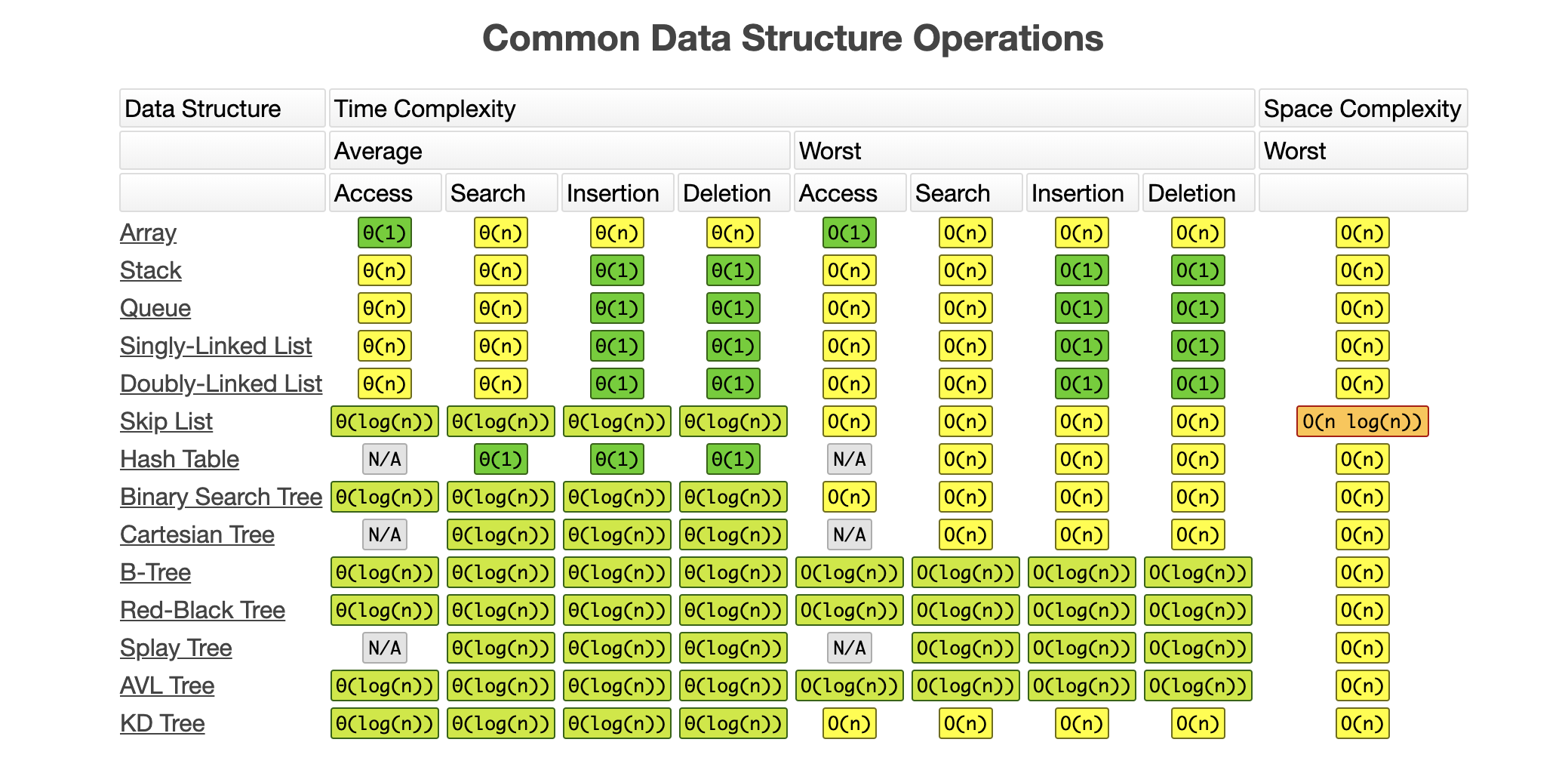
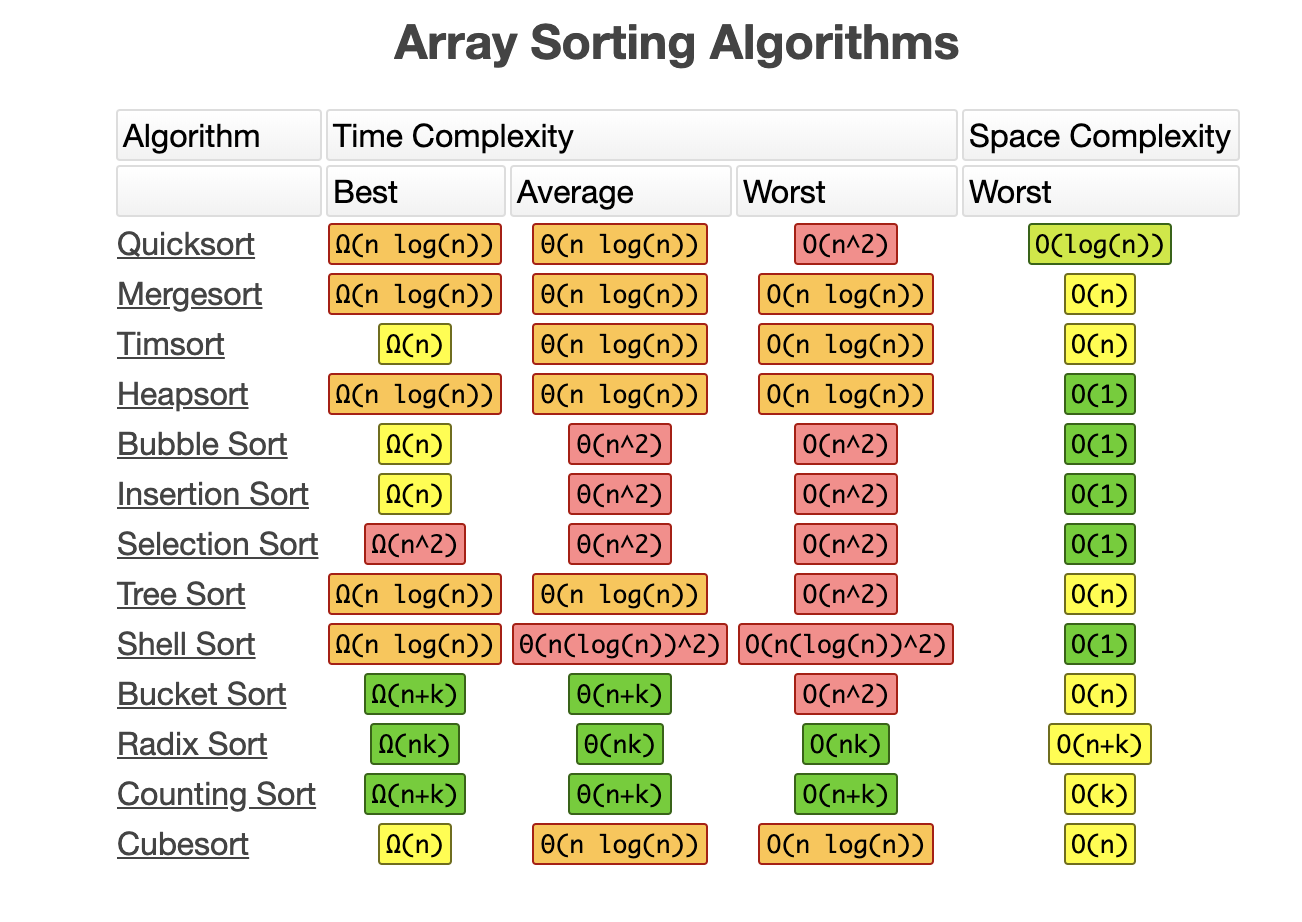
Complexity Cheat Sheets:

Source: www.bigocheatsheet.com

Complexity Chart

Common Data Structure Operations

Array Sorting Algorithms

Download as PDF from www.souravsengupta.com

Discussion

How we can compare the runtime characteristics of an algorithm or operations in a Data Structure

We could use The Big O Notation to measure the performance of the algorithms, so that we can compare them.

What means “to describe to runtime characteristics”

You should calculate the time (or memory) complexity of the algorithm or so called “Big O Notation”.

How to calculate the time (or memory) complexity

Just memorize the cheat sheets with the complexity of most common operations/ algorithms. Remember the order of the complexity types in terms of efficiency and be careful if you have one or multiple collections.

Examples

Check the sources for examples.

▪ Logarithmic algorithm – O(logn) – Binary Search
▪ Linear algorithm – O(n) – Linear Search
▪ Superlinear algorithm – O(nlogn) – Heap Sort, Merge Sort
▪ Polynomial algorithm – O(n^c) – Strassen’s Matrix Multiplication, Bubble Sort, Selection Sort, Insertion Sort, Bucket Sort
▪ Exponential algorithm – O(c^n) – Tower of Hanoi
▪ Factorial algorithm – O(n!) – Determinant Expansion by Minors, Brute force Search algorithm for Traveling Salesman Problem